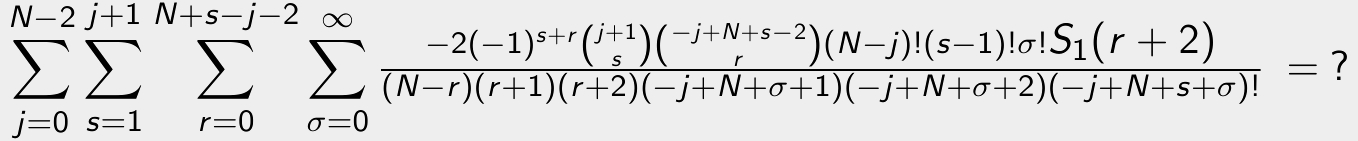The Computer Algebra and
Applications Group at RISC (team
leader: Carsten
Schneider) aims at developing flexible and efficient
symbolic summation and integration techniques, as well as
special function algorithms that assist in the calculation
of Feynman integrals arising in the context of Elementary
Quantum Field Theory.
This goal is attacked in intensive cooperation with the
Theory Group of the Deutsches Elektronen Synchrotron DESY,
Zeuthen (team leaders: Johannes Blümlein and Peter Marquard). A cooperation
contract between the Johannes Kepler University (JKU) and
DESY was signed in February 2007 and has been prolonged
step-wise till February 2026.
Beyond the application of these methods, algorithms and
tools in Quantum Field Theory, the group applies these
methods also in other fields, such as combinatorics
(simplification of enumerative problems) or number theory
(multiple zeta values, irrationality proofs, new relations
between sums).