|
The Algebraic View
Given a polynomial equation in three variables we want the general
solution in terms of rational functions in two variables.
For a linear equation like
x+y+z=1
the solution is always trivial, in this case:
(x, y, z) = (s, t, 1-s-t)
But when the equation is not linear, things become much more complicated.
For instance, the solutions of the equation
x2+y2+z2=1
can be parametrized by
(x, y, z) =
| 2s |
2t |
s2+t2-1 |
| -------- , |
-------- , |
-------- |
| s2+t2+1 |
s2+t2+1 |
s2+t2+1 |
except for the solution (0, 0, 1).
|
|
The Geometric Meaning
Geometrically speaking, an equation in three variables
defines a surface. And we are looking for a map from the
plan onto the surface.
The equation
x2+y2+z2=1
describes the unit sphere. The given parametrization
on the left side describes the stereographic projection
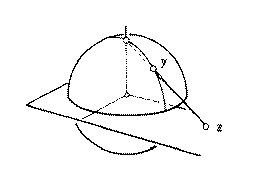mapping each point Z=(s,t) in the plane to a point Y=(x,y,z)
on the sphere. Each point on the sphere is reached
exactly once (except for the "north pole" (0,0,1) that is not
reached at all). Such a parametrization is called proper.
|
|
The Questions
For the solution set of a polynomial equation mainly three problems arise:
- First of all a (global) parametrization of the
solution set need not exist. So how to decide parametrizibility?
- But even if one knows that a rational parametrization exists, it can
be hard to find it. So how to find a parametrization?
- Furthermore, there will often be no one-one correspondence
between the parameter space (s,t) and the solution
set. A "small" subset of solutions may not be generated or
solutions may not be generated uniquely.
|
|
The Answers briefly
The answers depend on the underlying field. For the rationals
the answers were found just recently (Schicho, Jan. 2000).
- Over the complex the existence of a parametrization of an algebraic surface can be decided
by Castelnuovo's criterion, known for more than 100
years. Over the reals or the rationals additional conditions
are needed.
- Any parametrizable surface can be transformed to one out of a
finite number of special kinds of surfaces, for which strategies
for parametrization are known. The missing gaps were filled
by J. Schicho.
- Missing solutions are usually neglected. The uniqueness of
the rest of the solution set leads to the problem of
proper parametrization, which is both decidable and
computable.
|
