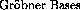



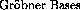
In the univariate case the 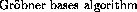 specializes to the Euclidean algorithm for
computing the greatest common divisor of polynomials. For
this reason, numerical GCD algorithms may yield insight into the problem of
numerical
specializes to the Euclidean algorithm for
computing the greatest common divisor of polynomials. For
this reason, numerical GCD algorithms may yield insight into the problem of
numerical 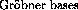 computation. Note that the numerical GCD routine described in
Section 2 ([\protect
computation. Note that the numerical GCD routine described in
Section 2 ([\protect ]) does not qualify for this purpose
since it only computes approximations of the roots of the GCD, not an
approximation of the polynomial itself.
]) does not qualify for this purpose
since it only computes approximations of the roots of the GCD, not an
approximation of the polynomial itself.
In [\protect ] a method for computing approximate GCDs based on the
Euclidean algorithm is presented in the context of approximate square-free
decomposition of polynomials. Some rules for detection of zero-coefficients
and normalization of polynomials that may also be applicable in the case of
numerical
] a method for computing approximate GCDs based on the
Euclidean algorithm is presented in the context of approximate square-free
decomposition of polynomials. Some rules for detection of zero-coefficients
and normalization of polynomials that may also be applicable in the case of
numerical 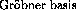 computation are given there.
computation are given there.
A different approach to numerical GCDs based on singular value decomposition
is presented in [\protect ]. There - in the univariate case -
the degree of the GCD is computed from the singular values of the polynomials'
sylvester matrix. A GCD is then computed by a Euclidean
algorithm, which terminates as soon as the degree of the remainder is equal to
the pre-determined degree. The problem of multivariate GCDs is reduced to the
univariate case by interpolation. In this method the input is assumed to have
limited accuracy. The GCD computed is then the exact result for a certain nearby problem. Additionally, it can be determined from the singular
values, by how much the input has to be perturbed at least
]. There - in the univariate case -
the degree of the GCD is computed from the singular values of the polynomials'
sylvester matrix. A GCD is then computed by a Euclidean
algorithm, which terminates as soon as the degree of the remainder is equal to
the pre-determined degree. The problem of multivariate GCDs is reduced to the
univariate case by interpolation. In this method the input is assumed to have
limited accuracy. The GCD computed is then the exact result for a certain nearby problem. Additionally, it can be determined from the singular
values, by how much the input has to be perturbed at least  this is the
exact result.
this is the
exact result.
This is similar to [\protect ], where these ideas are also applied for an
approach to numerical
], where these ideas are also applied for an
approach to numerical  computation. As originally invented in
[\protect
computation. As originally invented in
[\protect ] and elaborated further in [\protect
] and elaborated further in [\protect ] the idea of investigating the embedded problem is applied for the Euclidean
algorithm, finding the square-free decomposition of polynomials, and the
] the idea of investigating the embedded problem is applied for the Euclidean
algorithm, finding the square-free decomposition of polynomials, and the 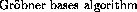 .
Like in [\protect
.
Like in [\protect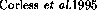 ] a nearby problem is solved and an upper bound for
the distance from the original problem is given. Basically, the results
differ just in the fact that in [\protect
] a nearby problem is solved and an upper bound for
the distance from the original problem is given. Basically, the results
differ just in the fact that in [\protect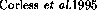 ] the euclidean 2-norm is used to
measure the distance between two coefficient vectors whereas in [\protect
] the euclidean 2-norm is used to
measure the distance between two coefficient vectors whereas in [\protect ]
the 1-norm is used.
]
the 1-norm is used.
Although the results seem very similar the method used is completely
different. The idea is (briefly) the following: one computes a polynomial
remainder sequence starting from the polynomials 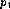 and
and 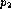 as usual and
performs additional polynomial computations - similar to the computation of
cofactors in the extended Euclidean algorithm - to maintain polynomials
as usual and
performs additional polynomial computations - similar to the computation of
cofactors in the extended Euclidean algorithm - to maintain polynomials
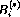 (for
(for 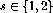 ),
), 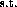

These ``cofactors'' can then be used for a termination criterion, since, if

we set

and know that then 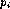 is the exact GCD of the perturbed polynomials
is the exact GCD of the perturbed polynomials
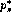 . Moreover, we know an upper bound of the perturbation of the
coefficients of the input polynomials, namely
. Moreover, we know an upper bound of the perturbation of the
coefficients of the input polynomials, namely  .
.
 Algorithms
Algorithms
Similar ideas to those employed for the numerical version of the Euclidean
algorithm are applied to the  as well, see also [\protect
as well, see also [\protect ]. If
S-polynomial
]. If
S-polynomial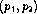 reduces to a non-zero polynomial
reduces to a non-zero polynomial  with
with 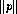 ``small'', then there might be polynomials
``small'', then there might be polynomials 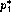 and
and 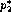 within
the input accuracy (
within
the input accuracy (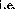 ``near''
``near'' 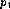 and
and 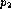 ),
), 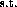 S-polynomial
S-polynomial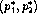 reduces to 0. Hence,
reduces to 0. Hence,  is eliminated! In
the case where a reduction yields a polynomial
is eliminated! In
the case where a reduction yields a polynomial 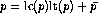 with ``small'' leading coefficient (compared to the remaining coefficients!)
only
with ``small'' leading coefficient (compared to the remaining coefficients!)
only 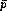 is adjoined to the basis and it is assumed that a perturbation
of the input polynomials would have this effect.
is adjoined to the basis and it is assumed that a perturbation
of the input polynomials would have this effect.
Such a generalized 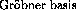 need not necessarily contain the same
monomials
need not necessarily contain the same
monomials as the
exact
as the
exact 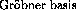 . This means that such a generalized
. This means that such a generalized 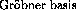 does not contain as much
information as the exact
does not contain as much
information as the exact 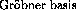 . For instance, it cannot be used to determine a
vector space basis of the residue class ring modulo an ideal, since, for this
purpose, we must rely on the leading monomials of the polynomials in the
basis. However, these methods can be very useful for solving systems of
equations, where the exact structure of the
. For instance, it cannot be used to determine a
vector space basis of the residue class ring modulo an ideal, since, for this
purpose, we must rely on the leading monomials of the polynomials in the
basis. However, these methods can be very useful for solving systems of
equations, where the exact structure of the 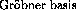 is not the main aspect. In
particular, if already the input is not known exactly, these methods can be
very helpful or, even more, the only meaningful to do.
is not the main aspect. In
particular, if already the input is not known exactly, these methods can be
very helpful or, even more, the only meaningful to do.
 Conserving Structure Information
Conserving Structure Information
In the case where the input is known exactly ( rational or integer
coefficients) floating point arithmetic could be used during the
rational or integer
coefficients) floating point arithmetic could be used during the 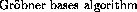 in
order to avoid coefficient growth and therefore to speed up computations.
Still, a result that contains all structural information about the
ideal would be desirable in this case.
in
order to avoid coefficient growth and therefore to speed up computations.
Still, a result that contains all structural information about the
ideal would be desirable in this case.
An approach towards this goal is described in [\protect ]. It should be
applicable in those cases as well where the structure of the
]. It should be
applicable in those cases as well where the structure of the 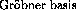 must
be known in order to solve the problem at hand. As already mentioned in
Section 3.2.1
must
be known in order to solve the problem at hand. As already mentioned in
Section 3.2.1 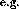 the computation of a vector space basis of
the residue class ring modulo an ideal, which in turn can be used to decide
whether a system of equations has finitely many solutions or not, is such a
case. Obviously, the correct detection of zero reductions is crucial to obtain
the desired result. The main features of their algorithm are
the computation of a vector space basis of
the residue class ring modulo an ideal, which in turn can be used to decide
whether a system of equations has finitely many solutions or not, is such a
case. Obviously, the correct detection of zero reductions is crucial to obtain
the desired result. The main features of their algorithm are
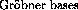 with floating point
coefficients, which converges to an exact
with floating point
coefficients, which converges to an exact 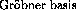 in a certain sense.
in a certain sense.
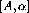 of precision
of precision  is a pair of
floating point numbers
is a pair of
floating point numbers  and
and  with precision
with precision  , where
, where  is an
approximation of a true coefficient and
is an
approximation of a true coefficient and  represents an error term.
Arithmetic for bracket coefficients is defined similar to interval arithmetic,
see [\protect
represents an error term.
Arithmetic for bracket coefficients is defined similar to interval arithmetic,
see [\protect ] or [\protect
] or [\protect ]. Arbitrary precision floating point
arithmetic is used, a round-off to precision
]. Arbitrary precision floating point
arithmetic is used, a round-off to precision  is simulated, and the error
made thereby is stored in the respective error term.
is simulated, and the error
made thereby is stored in the respective error term.
The crucial notion for convergence is supportwise convergence. The following notions are introduced: the monomial support of a polynomial are the monomials with non-zero coefficients, the monomial support of a polynomial set is the set of monomial supports of the individual polynomials. A sequence of polynomials converges coefficientwise if and only if, for each term, the sequence of coefficients converges. It converges supportwise if and only if starting from a certain index the monomial support does not change anymore and (from this index on) the sequence converges coefficientwise. Consequently, a set of polynomials converges supportwise if and only if the individual polynomials converge supportwise.
The algorithm then computes a sequence 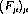 of polynomial sets with bracket coefficients of
increasing precision that converges supportwise to an exact
of polynomial sets with bracket coefficients of
increasing precision that converges supportwise to an exact 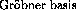 . Thus, there
is an index
. Thus, there
is an index 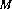
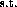 for each
for each 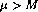 the support of the polynomial set is
equal to the support of the exact
the support of the polynomial set is
equal to the support of the exact 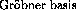 . Such a polynomial set is then called a
floating point
. Such a polynomial set is then called a
floating point 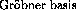 or simply approximate
or simply approximate 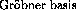 . There is,
however, no indication when this critical index
. There is,
however, no indication when this critical index  is reached during the
computation of the sequence. In other words: we don't know how far we have to
increase the precision
is reached during the
computation of the sequence. In other words: we don't know how far we have to
increase the precision  to be sure that we find a
to be sure that we find a 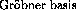 that contains the correct monomials.
that contains the correct monomials.


