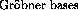 can be used to find exact solutions of systems of algebraic equations,
can be used to find exact solutions of systems of algebraic equations,
 [\protect
[\protect ], [\protect
], [\protect ], [\protect
], [\protect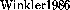 ], [\protect
], [\protect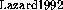 ], or
[\protect
], or
[\protect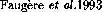 ]. Basically, the method consists of two steps:
]. Basically, the method consists of two steps:



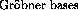 can be used to find exact solutions of systems of algebraic equations,
can be used to find exact solutions of systems of algebraic equations,
 [\protect
[\protect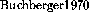 ], [\protect
], [\protect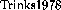 ], [\protect
], [\protect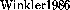 ], [\protect
], [\protect ], or
[\protect
], or
[\protect ]. Basically, the method consists of two steps:
]. Basically, the method consists of two steps:
 and then
and then
 ] and [\protect
] and [\protect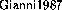 ]. Numerical variants
of this method might be investigated in case
]. Numerical variants
of this method might be investigated in case
In order to compute numerical solutions of a system of equations one can
employ floating point arithmetic in both steps of the solution method sketched
above. [\protect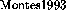 ] describes an approach where the first step is assumed to
be carried out already,
] describes an approach where the first step is assumed to
be carried out already,  from a given lexicographic
from a given lexicographic 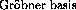 the step of
``successive elimination'' is carried out numerically. For every root a
condition number is introduced, from which a confidence interval containing
the exact root can be computed. The following numerical GCD routine is used
during the ``successive elimination'' step
the step of
``successive elimination'' is carried out numerically. For every root a
condition number is introduced, from which a confidence interval containing
the exact root can be computed. The following numerical GCD routine is used
during the ``successive elimination'' step : for each polynomial
we define a numerical solution as the union of the confidence
intervals of the computed roots, the numerical GCD of a set of
polynomials should then be the intersection of the numerical solutions of
the polynomials in the set.
: for each polynomial
we define a numerical solution as the union of the confidence
intervals of the computed roots, the numerical GCD of a set of
polynomials should then be the intersection of the numerical solutions of
the polynomials in the set.
Purely numerical methods for solving systems of polynomial equations have also
been studied in [\protect ] and [\protect
] and [\protect ], although the latter was
inspired by a stability analysis of the
], although the latter was
inspired by a stability analysis of the  . Basically, the problem is
reformulated as a matrix eigenproblem, which is then attacked
numerically. Altough the method presented there was improved in [\protect
. Basically, the problem is
reformulated as a matrix eigenproblem, which is then attacked
numerically. Altough the method presented there was improved in [\protect ]
it was not developed further. Still, starting from an exact
]
it was not developed further. Still, starting from an exact  the
connection between solutions of polynomial equations and matrix eigenproblems
has been studied in [\protect
the
connection between solutions of polynomial equations and matrix eigenproblems
has been studied in [\protect ] and [\protect
] and [\protect ].
].
However, all those approaches were aimed at a numerical solution of the system of equations rather than a numerical variant of the ``triangularization step'' in the exact method.


