 play a central role in polynomial ideal theory. They were originally
introduced in [\protect
play a central role in polynomial ideal theory. They were originally
introduced in [\protect ], for an introductory presentation of the concept
and some applications see [\protect
], for an introductory presentation of the concept
and some applications see [\protect ] and [\protect
] and [\protect ].
].



 play a central role in polynomial ideal theory. They were originally
introduced in [\protect
play a central role in polynomial ideal theory. They were originally
introduced in [\protect ], for an introductory presentation of the concept
and some applications see [\protect
], for an introductory presentation of the concept
and some applications see [\protect ] and [\protect
] and [\protect ].
].
For a given finite set of polynomials  a
a 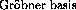
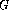 of the ideal generated
by
of the ideal generated
by  can be algorithmically constructed by the so-called
can be algorithmically constructed by the so-called 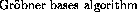 . The original
. The original
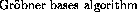 was given for sets of polynomials over an arbitrary field
was given for sets of polynomials over an arbitrary field 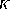 ,
generalizations of the algorithm have been investigated though for other
coefficient domains, in particular for Noetherian rings, see [\protect
,
generalizations of the algorithm have been investigated though for other
coefficient domains, in particular for Noetherian rings, see [\protect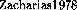 ],
Euclidean rings, see [\protect
],
Euclidean rings, see [\protect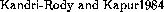 ] and [\protect
] and [\protect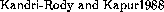 ], and for reduction
rings, see [\protect
], and for reduction
rings, see [\protect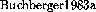 ] and [\protect
] and [\protect ].
].
We now want to focus on rational numbers as coefficient field,  we try to
compute
we try to
compute 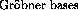 for ideals in
for ideals in 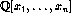 . Similar to the Euclidean
algorithm for computing greatest common divisors (GCDs) of polynomials in
. Similar to the Euclidean
algorithm for computing greatest common divisors (GCDs) of polynomials in
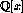 the
the 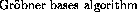 suffers from an intermediate swell of coefficients. This
means that the rational numbers occurring during the computation become very
large in size, which causes very time consuming arithmetic operations on the
coefficients. This in turn is due to the fact that rational number arithmetic
employs computation of GCDs of numerator and denominator, whose costs depend
on the length of the numbers involved.
suffers from an intermediate swell of coefficients. This
means that the rational numbers occurring during the computation become very
large in size, which causes very time consuming arithmetic operations on the
coefficients. This in turn is due to the fact that rational number arithmetic
employs computation of GCDs of numerator and denominator, whose costs depend
on the length of the numbers involved.
While theoretical investigations on the complexity of the 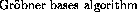 have assumed
constant time for all operations in the coefficient domain, see [\protect
have assumed
constant time for all operations in the coefficient domain, see [\protect ]
and [\protect
]
and [\protect ], the total computation time is in practice very often
dominated by arithmetic in the coefficient domain, see [\protect
], the total computation time is in practice very often
dominated by arithmetic in the coefficient domain, see [\protect ]. In the
case of rational number coefficients this problem can be attacked by modular
techniques, see [\protect
]. In the
case of rational number coefficients this problem can be attacked by modular
techniques, see [\protect ], [\protect
], [\protect ], [\protect
], [\protect ], and
[\protect
], and
[\protect ], or by approximate floating point arithmetic.
], or by approximate floating point arithmetic.
Several approaches - with different goals and motivations - for using floating point coefficients have been made so far.


