Integration in geschlossenen Ausdrücken

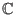
Definition 6   Ein Differentialkörper ist eine Menge von komplex-analytischen Funktionen, definiert auf einer offenen Teilmenge von $\mathbb{C}$ , die abgeschlossen ist bezüglich arithmetischen Operationen und Ableitung, und die die Menge der rationalen Funktionen enthält.

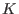
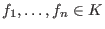
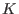
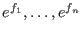
Definition 7   Es sei $K$ ein Differentialkörper, $f_1,\dots,f_n\in K$ ungleich 0 . Dann heißt der Körper, der von $K$ und $e^{f_1},\dots,e^{f_n}$ erzeugt wird, eine exponentielle Erweiterung von $K$ .

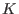
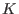
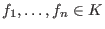
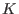
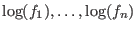
Definition 8   Es sei $K$ ein Differentialkörper, $f_1,\dots,f_n\in K$ ungleich 0 . Dann heißt der Körper, der von $K$ und $\log(f_1),\dots,\log(f_n)$ erzeugt wird, eine logarithmische Erweiterung von $K$ .

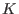
Definition 9   Eine reelle oder komplexe Funktion heißt elementar, wenn sie in einer iterierten [exponentiellen oder logarithmischen] Erweiterung des Differentialkörpers der rationalen Funktionen enthalten ist.

Satz 4 (Liouville)   Es sei $K$ ein Differentialkörper, $f\in K$ . Wenn $f$ eine Stammfunktion in einer iterierten [exponentiellen oder logarithmischen] Erweiterung besitzt, dann hat $f$ bereits eine Stammfunktion in einer logarithmischen Erweiterung.

Der Risch-sche Algorithmus entscheidet, ob eine gegebene elementare Funktion eine elementare Stammmfunktion hat, und rechnet eine solche aus im Fall daß eine existiert. Eine wesentliche Grundlage des Risch-schen Algorithmus ist die Partialbruchzerlegung von rationalen Funktionen.

Literatur:

[1]