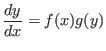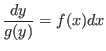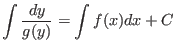Trennung der Variablen

Satz 2   Es seien $(a,b)$ und $(c,d)$ reelle Intervalle. Es seien $f:(a,b)\to\mathbb{R}$ und $g:(c,d)\to\mathbb{R}$ stetige Funktionen, $g(y)\ne 0$ für alle $y\in (c,d)$ . Es sei $F:(a,b)\to\mathbb{R}$ und $G:(c,d)\to\mathbb{R}$ Stammfunktionen von $f$ und $\frac{1}{g}$ . Dann sind die Lösungen der Differentialgleichung

$$y'(x) = f(x) g(y(x))$$

die Funktionen der Form $y(x)=G^{-1}(F(x)+C)$ , wobei $C\in\mathbb{R}$ eine Konstante ist, die so gewählt ist, daß $F(x)+C$ im Wertebereich von $G$ liegt.

Abgekürzte Schreibweise:

$$\frac{dy}{dx} = f(x) g(y)$$

$$\frac{dy}{g(y)} = f(x) dx$$

$$\int \frac{dy}{g(y)} = \int f(x) dx + C$$

$$G(y) = F(x) + C$$

$$y = G^{-1}(F(x) + C)$$

Diese Schreibweise soll nur die rechnerische Durchführung der Methode der Trennung der Variablen erleichtern, als mathematische Herleitung der Lösung ist sie nicht geeignet, da mehrere Zwischenschritte offensichtlich formal fehlerhaft sind (angefangen damit, daß 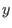$y$ gleichzeitig als numerische Variable und als Funktionsvariable auftritt).

Satz 3   Die ``Euler-homogene Differentialgleichung''

$$y'(x) = f\left( \frac{y}{x} \right)$$

läßt sich durch die Transformation 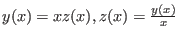$y(x)=xz(x), z(x)=\frac{y(x)}{x}$ auf eine Gleichung zurückführen, bei der die Variablen getrennt werden können.

Literatur:

[3, II.8,II.9]