Es sei
![]() ein beschränktes Intervall,
ein beschränktes Intervall,
![]() stetig differenzierbar,
stetig differenzierbar,
![]() .
Unter den Funktionen
.
Unter den Funktionen
![]() , die die Randbedingung
, die die Randbedingung
![]() erfüllem sucht man eine,
die das Integral
erfüllem sucht man eine,
die das Integral
![]() minimieren. Für Lösungen dieses
Variationsproblems gibt der folgende Satz eine notwendige Bedingungung an.
minimieren. Für Lösungen dieses
Variationsproblems gibt der folgende Satz eine notwendige Bedingungung an.
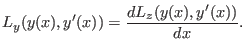
![$\displaystyle I'(0)=\int_a^b [ L_y(y(x),y'(x))h(x)+L_z(y(x),y'(x))h'(x)] dx $](img436.png)
![$\displaystyle = \int_a^b \left [L_y(y(x),y'(x)) - \frac{dL_z(y(x),y'(x))}{dx}\right] h(x)dx , $](img437.png)
wobei man verwendet daß der erste Summand in der partiellen Integration wegen
Ein einfaches Beispiel ist das Problem der kürzesten Verbindung. Hier wählt man
![]() . Die Euler-Lagrange-Gleichung ist
. Die Euler-Lagrange-Gleichung ist ![]() . Die Lösung ist natürlich die
Gerade.
. Die Lösung ist natürlich die
Gerade.
Ein weiteres Beispiel ist das Problem der schnellsten Verbindung (Brachystochrone) unter dem Einfluß
der Schwerkraft: am Punkt ![]() ist die Geschwindigkeit
ist die Geschwindigkeit
![]() , wobei
, wobei ![]() die Erdbeschleunigung ist.
Man setzt
die Erdbeschleunigung ist.
Man setzt
![]() . Die Euler-Lagrange-Gleichung ist
. Die Euler-Lagrange-Gleichung ist
![]() .
Die Lösungskurve ist eine Zykloide, mit der Parameterdarstellung
.
Die Lösungskurve ist eine Zykloide, mit der Parameterdarstellung
Variationsprobleme mit einer Nebenbedingung der Art
![]() , wobei
, wobei
![]() stetig differenzierbar ist und
stetig differenzierbar ist und
![]() ist, können mit der Methode des Lagrange-Multiplikators behandelt
werden. Sie führt auf die Gleichung
ist, können mit der Methode des Lagrange-Multiplikators behandelt
werden. Sie führt auf die Gleichung
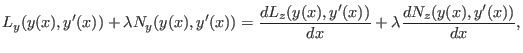
wobei