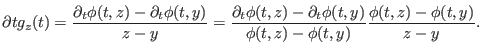Nächste Seite: Analyse von Gleichgewichtspunkten
Aufwärts: Sätze und Definitionen
Vorherige Seite: Folgerungen aus Picard/Lindelöf
Es sei
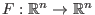 ein stetig differenzierbares Vektorfeld
mit beschränkter Ableitung (damit die Lipschitz-Bedingung erfüllt ist).
Es sei
ein stetig differenzierbares Vektorfeld
mit beschränkter Ableitung (damit die Lipschitz-Bedingung erfüllt ist).
Es sei
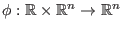 die Abbildung, die durch die
Bedingungen
die Abbildung, die durch die
Bedingungen
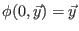 for all
for all
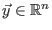 ,
,
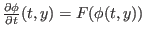 definiert ist.
Sie beschreibt die Lösung in Abhängigkeit von den Anfangswerten
und ist daher stetig. Sie erfüllt die Funktionalgleichung
definiert ist.
Sie beschreibt die Lösung in Abhängigkeit von den Anfangswerten
und ist daher stetig. Sie erfüllt die Funktionalgleichung
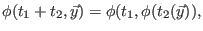 |
(8) |
insbesondere ist
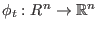 ,
,
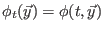 invertierbar
mit inverser Abbildung
invertierbar
mit inverser Abbildung 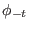 . Die Abbildung
. Die Abbildung 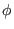 heißt Fluß
des Vektorfeldes
heißt Fluß
des Vektorfeldes
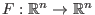 .
.
Wenn das Richtungsfeld 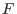 nicht Lipschitz-stetig ist, dann muß der Fluß
nicht überall definiert sein. Wenn
nicht Lipschitz-stetig ist, dann muß der Fluß
nicht überall definiert sein. Wenn 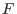 differenzierbar ist, dann ist die
Lipschitz-bedingung zumindest lokal auf jeder kompakten Teilmenge erfüllt,
und für jeden Punkt
differenzierbar ist, dann ist die
Lipschitz-bedingung zumindest lokal auf jeder kompakten Teilmenge erfüllt,
und für jeden Punkt
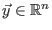 ist der Fluß lokal in einer
einen offenen Umgebung von
ist der Fluß lokal in einer
einen offenen Umgebung von
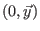 definiert.
definiert.
Satz 13
Es sei
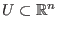 offen und
offen und
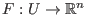 ein stetig differenzierbares
Vektorfeld. Dann ist der Fluß
ein stetig differenzierbares
Vektorfeld. Dann ist der Fluß 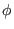 in seinem ganzen Definitionsbereich differenzierbar.
in seinem ganzen Definitionsbereich differenzierbar.
Beweis.
Es sei
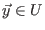
fix gewählt.
Es ist schon gezeigt, daß
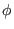
stetig
ist, außerdem existiert die ``Zeitableitung''
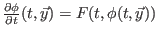
. Es reicht zu
zeigen, daß die ``Raumableitung''
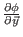
existiert
und stetig ist (der Wert der Raumableitung ist eine lineare Abbildung von
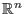
nach
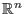
). Wir zeigen nur den Fall
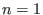
.
Es sei 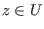 ,
,
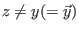 . Es ist zu zeigen, daß die parameterabhängige Funktion
. Es ist zu zeigen, daß die parameterabhängige Funktion
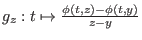 für
für 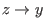 konvergiert (der Grenzwert ist dann die Raumableitung). Die Abbildung
konvergiert (der Grenzwert ist dann die Raumableitung). Die Abbildung
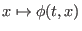 ist injektiv für alle
ist injektiv für alle 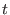 im Definitionsbereich, daher ist
im Definitionsbereich, daher ist
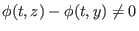 gilt. Es gilt
gilt. Es gilt
Mit der Definition
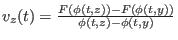
erfüllt
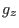
die Differenzialgleichung
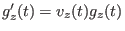
und die Anfangsbedingung
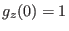
.
Dieses Anfangswertproblem ist linear, und nach Satz
12 ist der Grenzübergang
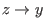
erlaubt. Da
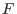
differenzierbar ist, ist
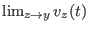
definiert und
gleich
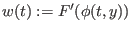
. Daher existiert auch die Raumableitung
als Lösung
des Anfangwertproblems
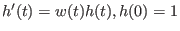
.

Definition 12
Es sei
eine positive ganze Zahl.
Es seien
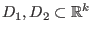
offene und zusammenhängende Mengen,
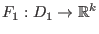
und
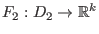
Vektorfelder,
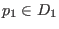
und
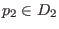
. Wir sagen
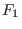 ist bei
ist bei 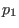 lokal topologisch äquivalent
zu
lokal topologisch äquivalent
zu 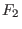 bei
bei 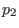
wenn für Umgebungen
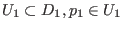
und ein Homöomorphimus
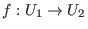
existiert, der jede Lösungskurve in eine Lösungskurve abbildet, und der auf den
Lösungskurven die lineare Ordnung erhält, die durch die Parametrisierung mit
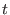
gegeben ist
(informell ausgedrückt: der das Phasenbild inklusive Richtung der Pfeile erhält).
Definition 13
Es sei
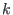
eine positive ganze Zahl,
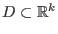
eine offene und zusammenhängende Menge,
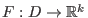
ein differenzierbares Vektorfeld, und
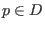
ein Punkt sodaß
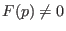
ist.
Eine Hyperebene
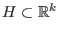
durch
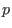
heißt transversal zu
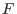
bei
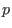
, wenn der Vektor
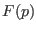
nicht in dem Vektorraum
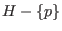
(Hyperebene
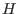
verschoben, sodaß die durch den Nullpunkt geht)
enthalten ist.
Satz 14
Es sei 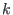 eine positive ganze Zahl,
eine positive ganze Zahl,
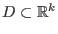 eine offene und zusammenhängende Menge,
eine offene und zusammenhängende Menge,
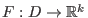 ein differenzierbares Vektorfeld, und
ein differenzierbares Vektorfeld, und 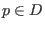 ein Punkt sodaß
ein Punkt sodaß 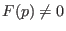 ist.
Dann ist
ist.
Dann ist 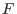 bei
bei 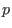 lokal äquivalent zum konstanten Vektorfeld
lokal äquivalent zum konstanten Vektorfeld
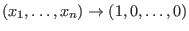 bei
bei
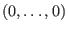 .
.
Beweis.
Es sei
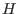
eine transversale Hyperebene. Dann ist die Flußabbildung
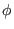
eingeschränkt auf
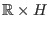
auf einer Umgebung von
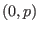
definiert und differenzierbar.
Die Jacobi-Matrix bei
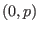
ist nicht singulär, daher ist die Abbildung ein lokaler
Homöomorphismus. Sie bildet die Lösungskurven des konstanten Vektorfelds (Geraden) auf Lösungskurven
von
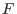
ab.

Es folgt, daß zwei Nicht-Gleichgewichtspunkte bei gleicher Dimension immer lokal äquivalent sind.
- Literatur:
- leider ist dieses Kapitel in keinem der beiden Bücher enthalten.



Nächste Seite: Analyse von Gleichgewichtspunkten
Aufwärts: Sätze und Definitionen
Vorherige Seite: Folgerungen aus Picard/Lindelöf
Josef Schicho
2016-01-17
![]() ein stetig differenzierbares Vektorfeld
mit beschränkter Ableitung (damit die Lipschitz-Bedingung erfüllt ist).
Es sei
ein stetig differenzierbares Vektorfeld
mit beschränkter Ableitung (damit die Lipschitz-Bedingung erfüllt ist).
Es sei
![]() die Abbildung, die durch die
Bedingungen
die Abbildung, die durch die
Bedingungen
![]() for all
for all
![]() ,
,
![]() definiert ist.
Sie beschreibt die Lösung in Abhängigkeit von den Anfangswerten
und ist daher stetig. Sie erfüllt die Funktionalgleichung
definiert ist.
Sie beschreibt die Lösung in Abhängigkeit von den Anfangswerten
und ist daher stetig. Sie erfüllt die Funktionalgleichung
![]() nicht Lipschitz-stetig ist, dann muß der Fluß
nicht überall definiert sein. Wenn
nicht Lipschitz-stetig ist, dann muß der Fluß
nicht überall definiert sein. Wenn ![]() differenzierbar ist, dann ist die
Lipschitz-bedingung zumindest lokal auf jeder kompakten Teilmenge erfüllt,
und für jeden Punkt
differenzierbar ist, dann ist die
Lipschitz-bedingung zumindest lokal auf jeder kompakten Teilmenge erfüllt,
und für jeden Punkt
![]() ist der Fluß lokal in einer
einen offenen Umgebung von
ist der Fluß lokal in einer
einen offenen Umgebung von
![]() definiert.
definiert.
![]() ,
,
![]() . Es ist zu zeigen, daß die parameterabhängige Funktion
. Es ist zu zeigen, daß die parameterabhängige Funktion
![]() für
für ![]() konvergiert (der Grenzwert ist dann die Raumableitung). Die Abbildung
konvergiert (der Grenzwert ist dann die Raumableitung). Die Abbildung
![]() ist injektiv für alle
ist injektiv für alle ![]() im Definitionsbereich, daher ist
im Definitionsbereich, daher ist
![]() gilt. Es gilt
gilt. Es gilt