Folgerungen aus Picard/Lindelöf

Satz 12   Es sei $n\in\mathbb{N}$ . Es seien $a_1,\dots,a_n,b:D\to\mathbb{R}$ stetige Funktionen, $x_0\in D$ , $y_0,\dots,y_{n-1}\in\mathbb{R}$ . Dann hat das Anfangswertproblem

$$y^{(n)}(x)+a_1(x)y^{(n-1)}(x)+\dots+a_n(x)y(x)=b(x), y(x_0)=y_0,\dots,y^{(n-1)}(x_0)=y_{n-1}$$

eine eindeutige Lösung.

Beweis. Auf jedem kompakten Teilintervall erfüllt die Funktion $F:D\times R^n\to\mathbb{R}^n$ ,

$$(x,y_0,\dots,y_{n-1})\mapsto (y_1,\dots,y_{n-1},b(x)-a_1(x)y_{n-1}-\dots-a_n(x)y_0)$$

eine Lipschitzbedingung. Daher kann man die vektorielle Version von Satz 11 anwenden. $\qedsymbol$

Aus dem Beweis (nicht in dieser Zusammenfassung enthalten) des Banachschen Fixpunktsatzes 10 erhält man die Abschätzung für die Entfernung zum Fixpunkt $\bar{x}$ :

$$d(x,\bar{x}) \le \frac{d(x,f(x))}{1-c} .$$

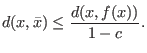
Diese Abschätzung erlaubt, die Genauigkeit einer Näherungslösung abzuschätzen.

Wir betrachten zum Beispiel das Euler'sche Polygonzugverfahren. Es sei $F:\mathbb{R}\to\mathbb{R}$ Lipschitz-stetig mit Lipschitz-Konstante $L$ . Es seien $a,b,y_0\in\mathbb{R}$ , $x_0\in [a,b]$ . Wir approximieren die Lösung des Anfangswertproblems $y'(x)=F(y(x))$ , $y(a)=y_0$ wie folgt: Zuerst wird das Intervall unterteilt in $N$ gleich große Teilintervalle. Wir setzen $h:=\frac{b-a}{N}$ , $x_i:=a+ih$ und für $i=0,\dots,N$ (d.h. $x_0=a,x_N=b$ ). DDann setzen wir $p_i=F(y_i)$ und $y_{i+1}:=y_i+p_ih$ für $i=0,\dots,N-1$ . Die approximierende Funktion ist nun die stückweise lineare Funktion $z$ , für die $z(x_i)=y_i$ gilt: im Intervall $x\in [x_i,x_{i+1}]$ ist $z(x)=y_i+p_i(x-x_i)$ . In jedem Intervall gilt die Abschätzung

$$\left\vert y_{i+1}-y_i-\int_{x_i}^{x_{i+1}}F(z(t))dt\right\vert = \left\vert F(y_i)h-\int_{x_i}^{x_{i+1}}F(z(t)))dt\right\vert =$$

$$\left\vert\int_{x_i}^{x_{i+1}}(F(y_i)-F(z(t))dt\right\vert \le L\left\vert\int_{x_i}^{x_{i+1}}(y_i)-z(t))dt\right\vert =$$

$$L\left\vert\int_{x_i}^{x_{i+1}} p_i(t-x_i) dt \right\vert = Lp_i\frac{h^2}{2}=\frac{Lp_i(b-a)^2}{2N^2} .$$

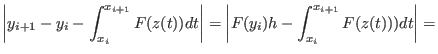
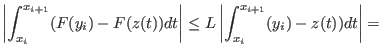
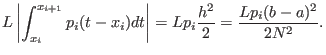
Die Distanz $d(z,P(z))$ kann abgeschätzt werden durch die Summe von höchstens $N$ der Teil-Abschätzungen, und das ist nach oben beschränkt durch $\frac{LM(b-a)^2}{2N}$ , wobei $M$ eine obere Schranke für $F$ ist. Für große $N$ geht der Fehler gegen Null.

Um die Abhängigkeit der Lösung vom Anfangswert zu untersuchen, nehmen wir an, daß $f,g$ beide die Differentialgleichung erfüllen, aber verschiedene Anfangswerte haben: $f(x_0)=y_0$ , $g(x_0)=z_0$ . Dann betrachtet man $g$ als Näherungslösung für das Anfangswertproblem mit Anfangsbedingung $y(x_0)=y_0$ und bekommt die Abschätzung $\vert f(x_1)-g(x_1)\vert\le\frac{\vert y_0-z_0\vert}{1-L\vert x_1-x_0\vert}$ im Fall daß der Nenner positiv ist. Andernfalls führt Unterteilung des Intervalls zu einer Abschätzung, die allerdings exponentiell in der Länge des Intervalls ist.

Die Stetigkeit in den Anfangsbedingung ist auch für den vektoriellen Fall erfüllt (mit einer ähnlichen Abschätzung).

Wenn die rechte Seite der Differentialgleichung stetig von Parametern abhängt, dann ist die Lösung ebenfalls stetig in den Parametern. Das läßt sich dadurch zeigen, daß man die Parameter als zusätzliche Koordinaten der gesuchten Funktion einführt, deren Ableitung konstant gleich 0 ist.

Literatur:

[3, III.13]